pta六度空间
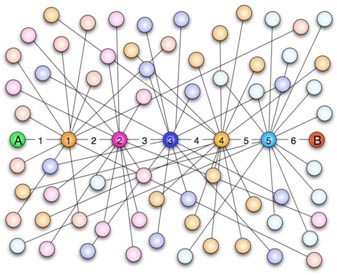
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图6.4所示。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式说明:
输入第1行给出两个正整数,分别表示社交网络图的结点数N (1<N<=104,表示人数)、边数M(<=33*N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式说明:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%一点理解:
时隔一个多月,再次做到此题目,发现并不会写了(并不是),甚至原来的题解,也不会写了,回想起来,自己还写过题解,特此更新。。。发现原来写的题解具有一定的局限性,并不是十分好理解,所以特此更新呢。
以下为原题解:
乍一看题目所求有些懵,其实所求的是每个节点相邻的6层之内的节点个数与总结点的比例;
那么我们只需要求出每个节点的相邻六层的节点的个数(bfs)
在bfs中我们还需要注意一下,我们在统计个数的时候还有记得数层数,够了层数就不再去数数了。
所以引申出来层数的判断,那么如何确定到那一层了呢?
采用的就是tail和last的不断更新(详见代码)
#include<bits/stdc++.h>
using namespace std;
const int maxn = 10005;
bool vis[maxn];//是否被访问过
vector<int> g[maxn];
int vertices, edges;//所有的顶点数和边数
int BFS(int v)
//返回该顶点在6度空间里的能接触到的顶点个数
{
for(int i=0;i<maxn;i++){
vis[i] = false;//init vis[]
}
int tail;
int last = v;//指的是每一圈的最后一个(每一个外圈的的每一个顶点都要入队,当该外圈的最后一个也出队了,那么这一层也循环完了
int count =1;
int level = 0;
vis[v] = true;
queue<int>q;
q.push(v);
while(!q.empty()){
int x = q.front();//get the first每一圈的每一个顶点
q.pop();
for(int j=0;j<g[x].size();j++){//判断条件是与x相连的所有顶点的个数
if(!vis[g[x][j]]){
vis[g[x][j]] = true;
q.push(g[x][j]);
tail = g[x][j];//每次都将替换更新,最后得到的是该节点的最后一个相连顶点
count++;
}
}
if(x==last){
/*这里指的是我们将该层全部弹出时应所满足的条件
注意第一次的时候是直接成立的
而在第二圈(或更多)的时候,我们将
第一个节点的最后一个遍历的节点作为tail
然后他就成为了last即上一层的最后一个元素
*/
last = tail;
level++;
}
if(level==6)break;
}
return count;
}
int main(){
int x,y;
cin>>vertices>>edges;
for(int i = 1;i<=edges;i++){
cin>>x>>y;
g[x].push_back(y);//建立两者之间边的关系
g[y].push_back(x);//认识是相互的,所以相互加关联
}
for(int j=1;j<=vertices;j++){
printf("%d: %.2f%%\n",j,BFS(j)*1.0/vertices*100.0);
}
return 0;
}下面是一个月后经过了几道[[bfs]]题目熏陶后的想法:
首先读题,发现题目要求我们输出比例,显然总结点数已经给出,那么得到每一个节点的6层以内的节点数即可。
接着题目有给定了节点之间的关系,所以我们自己可以通过一个bool类型的rel(relative)的二维数组来确定两者的关系是否连通。(这一步可以在main函数中实现)
int main(){
int x,y;
cin>>vertices>>edges;
memset(ral,false,sizeof(ral));
for(int i = 1;i<=edges;i++){
cin>>x>>y;
ral[x][y]=1;
ral[y][x]=1;
}接下来,我们就要把他传入bfs中了,然后使得bfs返回该节点符合关系的节点数目即可
for(int j=1;j<=vertices;j++){
printf("%d: %.2f%%\n",j,BFS(j)*1.0/vertices*100.0);在bfs 的函数中,我们很显然,起点就是我们给定的j,j即为起始点,由他出发寻找到在六层内不同的节点的个数。
从这个任务中我们也可得出一个状态的内容是它自身的节点名称(在此题目中是一个int值)还要有一个cnt来表示层数,方便我们作为层数的限制条件,这在其他的bfs题目中,层数亦十分有用。
struct node
{
int cnt;
int val;
};哦,我们不能忘我们刚刚给的要求了,不同的节点,相同的节点找他干嘛。。。所以还要有一个vis的一维数组,范围是所有节点数量,表示他们是否被访问过。
const int maxn = 1005;
int n,m;
bool vis[maxn];//是否被访问过
bool ral[maxn][maxn];那么bfs的结束条件是?队列结束或者达到节点6层。
int BFS(int v)
//返回该顶点在6度空间里的能接触到的顶点个数
{
int count=1;
memset(vis,false,sizeof(vis));
queue<node>q;
vis[v]=1;
node t;
t.cnt = 1;
t.val = v;
q.push(t);
while(!q.empty()){
node front = q.front();
q.pop();
if(front.cnt>6)break;
t.cnt = front.cnt+1;
for(int i=1;i<=vertices;i++){
if(ral[front.val][i]&&!vis[i]){
vis[i]=1;
count++;
t.val = i;
q.push(t);
}
}
}
return count;
}bfs里面的cnt>或是>=我是猜的,可以通过数据检验,稍微改改就凑上了。。省得麻烦考虑了,不过最好还是考虑周全。
在这里val的数据范围是[n] [n]或者说直接定义1001(因为题目给定的数据n<=10^3)。